Trochoids , hypocycloids and epicycloids
TROCHOIDS
A trochoid is obtained by following a point on the spoke of a wheel
as the wheel rolls in a straight line without slipping .
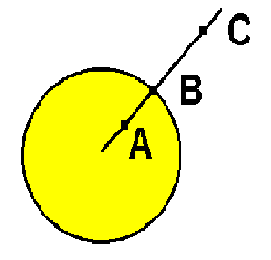
Consider a circle of radius R as it rolls in a straight line. Tracing the point A , which is a distance less than R along the spoke, produces a curtate cycloid.
Tracing the point B, which is exactly a distance R along the spoke, produces a cycloid.
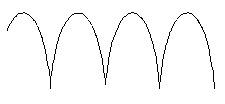
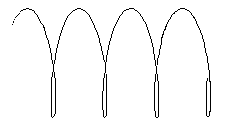
Tracing the point C, which is a distance greater than R along the spoke, produces a
prolate cycloid.
HYPOCYCLOIDS

Following the motion of a point P on a spoke of a circle of radius b, as it rolls without slipping on the inside of a second circle of radius a>b, produces a curve which is called a hypocycloid.
EPICYCLOIDS
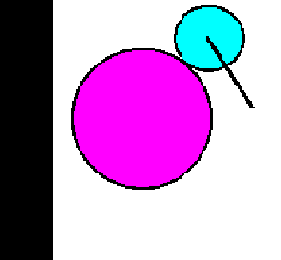
Following the motion of a point P on a spoke of a circle of radius b, as it rolls without slipping on the outside of a second circle of radius a>b, produces a curve which is called a epicycloid.
Gear teeth are frequently made to conform to the cycloid shape so that
there is more of a rolling rather than sliding contact when the gears mesh.