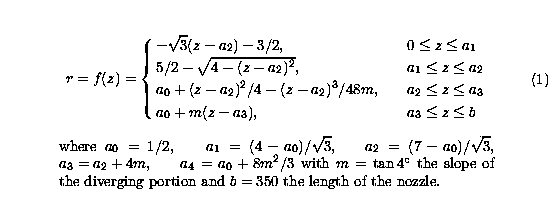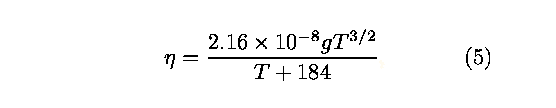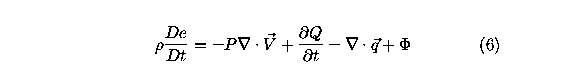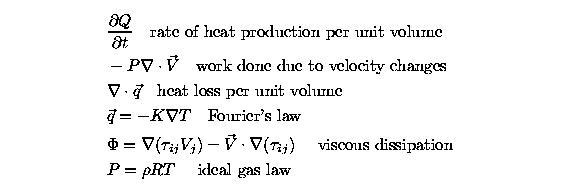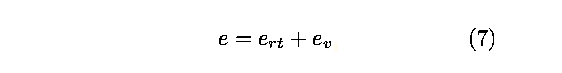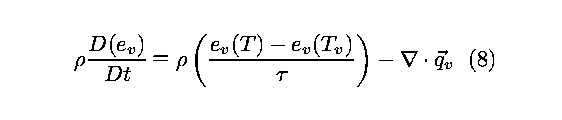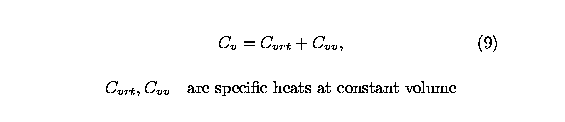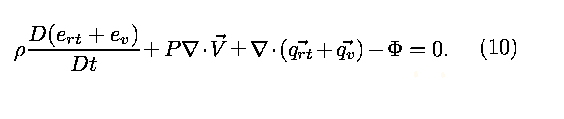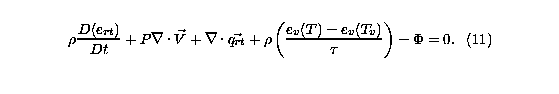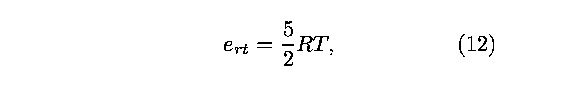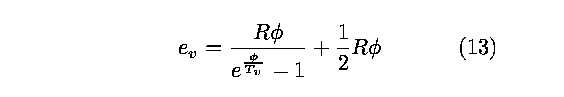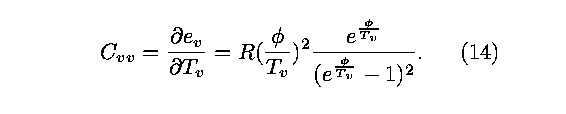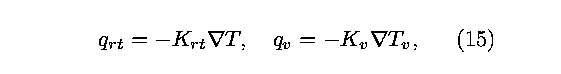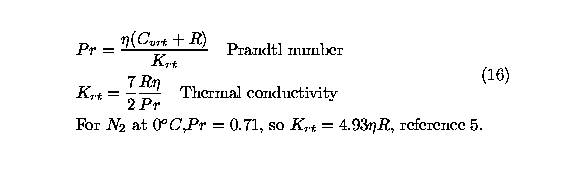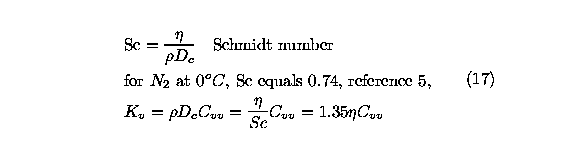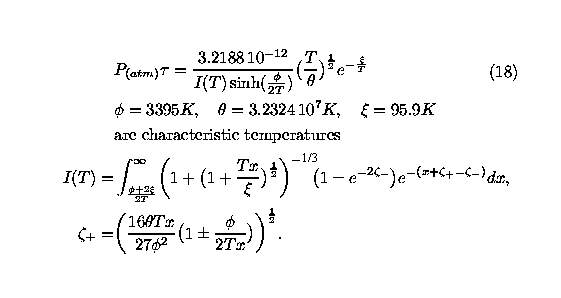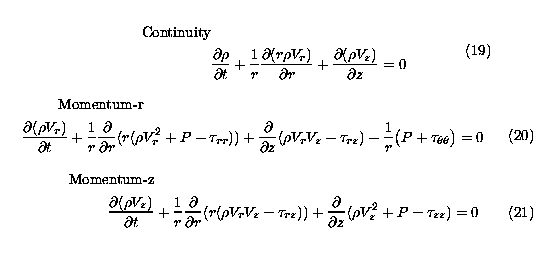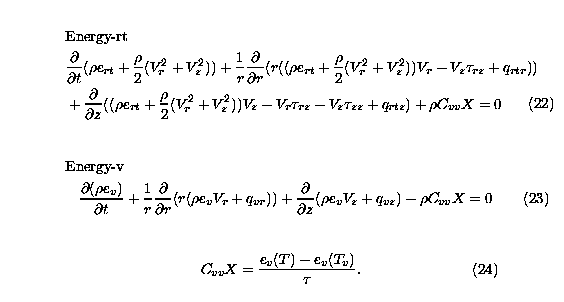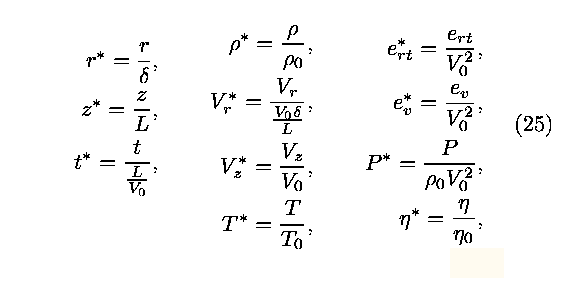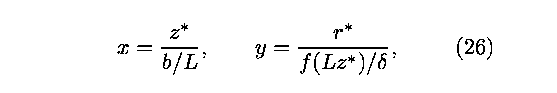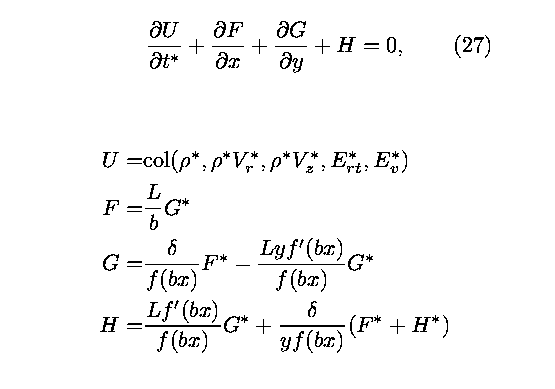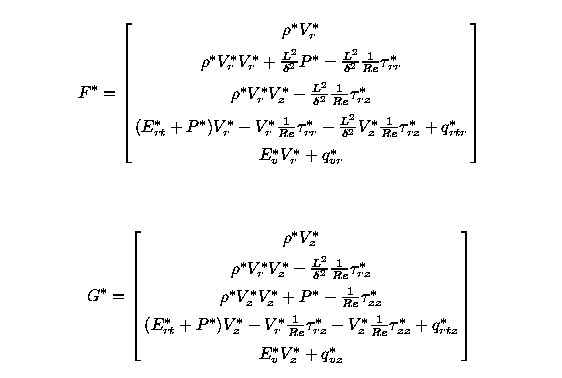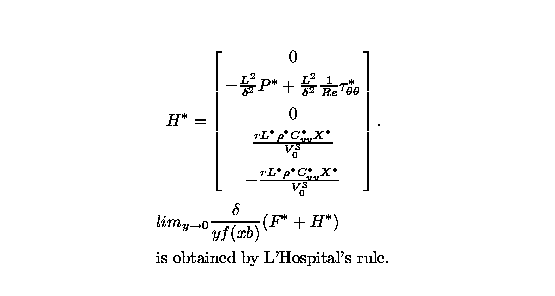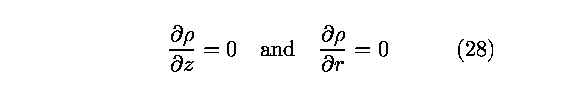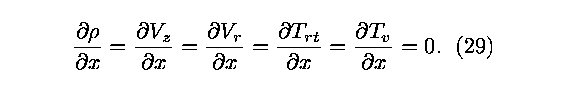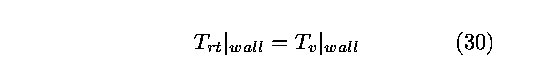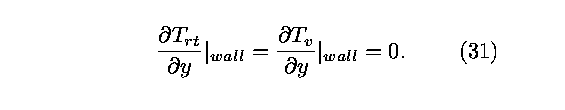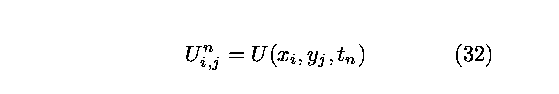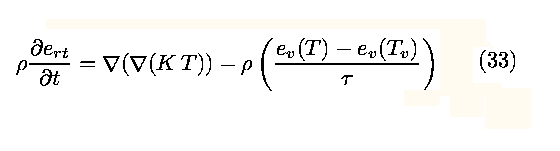NOZZLE FLOW WITH VIBRATIONAL NONEQUILIBRIUM

Abstract

The flow of high temperature nitrogen gas through a converging-diverging conical test nozzle is simulated under conditions of thermodynamical nonequilibrium. The flow is simulated using the Navier-Stokes equations that have been modified to include the effects of intermolecular forces and vibrational nonequilibrium. In particular, two energy equations are used. One energy equation accounts for energy effects due to translational and rotational degrees of freedom. The other energy equation models effects due to the vibrational degree of freedom. These energy equations are coupled using an improved relaxation time over the temperature range of the flow. The computational fluid dynamics algorithm of Steger-Warming flux vector splitting method was employed to solve the resulting equations. The equations were also solved using the implicit MacCormack method as a check of the computations. Both of these methods produced consistent numerical results. Our simulation showed that a uniform flow was produced outside the boundary layer and that nonequilibrium exists in both the converging and diverging nozzle sections. The boundary layer exhibited a marked increase in the translational-rotational temperature. The vibrational temperature, away from the boundary layer, remains essentially frozen downstream of the nozzle and along the center line.

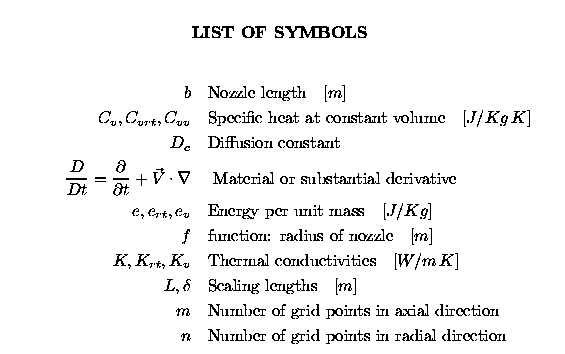
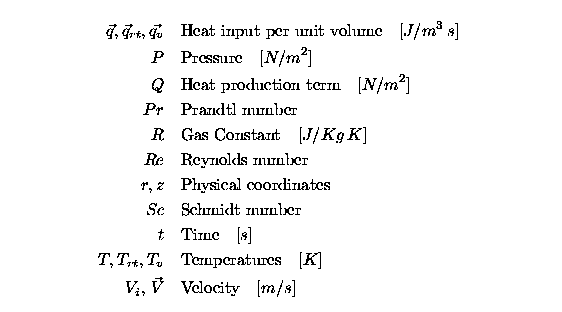
Introduction

Computational fluid dynamics is being used to design hypersonic wind tunnels and hypersonic vehicles, reference 1. Wind tunnels are important in aerothermodynamic research and knowledge of their flow quality is essential. Small conical test nozzles are also used in various research projects and their flow quality is also of importance. The research in reference 1 concluded that, for their nozzle shape, there was poor flow quality in a certain hypersonic nitrogen flow in a converging-diverging nozzle. The poor flow was attributed to nonequilibrium effects and expansion and compression waves crossing the nozzle exit plane. This raised the question, "What would be the flow quality in a conical test nozzle under conditions of thermal nonequilibrium?" In order to answer this question we considered the problem of flow quality of a high temperature nitrogen gas flowing through a high expansion converging-diverging conical test nozzle. This research differs from that of reference 1 in both the shape of the nozzle, the numerical solution techniques, boundary conditions and parameter values used in the modeling. This problem was investigated in the work performed in reference 2 and was motivated by concern of test nozzle behavior underconditions of thermodynamical nonequilibrium between the translational-rotational and vibrational degrees of freedom of the molecules. (This work was supported under research grant NAG-1-1424.) The modeling of nonequilibrium effects requires that the Navier Stokes equations be modified as they do not fully describe energy transfer for diatomic molecules like nitrogen at high temperatures. We therefore developed the necessary energy equations describing energy transfer between a translational-rotational energy mode and a vibrational energy mode. These energy equations are coupled using an improved relaxation time associated with this type of nonequilibrium nozzle flow over the temperature range considered.

NozzleShape

The equations which describe the converging-diverging conical test nozzle are defined in cylindrical coordinates with the z-axis representing the center line of the nozzle and symmetry existing in the theta direction. The nozzle shape is then described by the radius as a function of z, and is divided into four sections. Starting at the nozzle entrance the sections are described by a straight line, a circle, a cubic spline and another straight line. The location of the points separating each section are designated a1, a2 and a3. The nozzle radius in millimeters, is a function of the axial distance in millimeters, and is given by

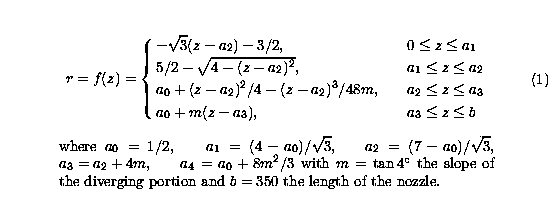
Governing Equations of Motion for equilibrium case

For conditions of equilibrium between the degrees of freedom of a gas one usually solves the Navier-Stokes equations, which consist of a continuity equation, momentum equations and an energy equation together with an equation of state, subject to given boundary and initial conditions. The conservation of mass is represented by
The conservation of momentum is obtained from the equations The coefficient of viscosity is calculated using the Sutherland formula for nitrogen, references 4,6. 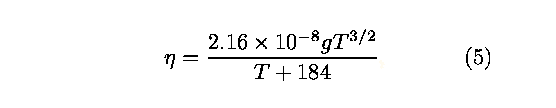where the temperature T is in degrees Rankine.

In a single temperature model, equilibrium exists among the degrees of freedom of the gas and so the change in the total energy of a fluid in motion is set equal to the changes in the internal energy, kinetic energy, work done, and heat from conduction. The internal energy per unit mass, e(T), is a function of temperature and satisfies

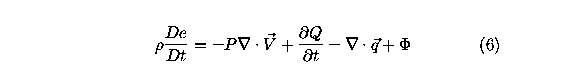
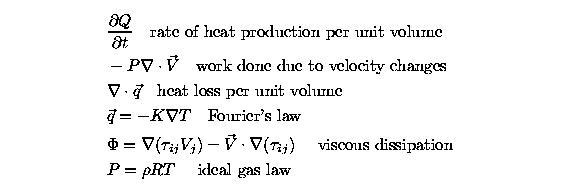
Nonequilibrium considerations

In contrast, under conditions of thermal nonequilibrium, we assume that initially the gas is such that two temperatures exist, one temperature representing the translational-rotational internal energy and another temperature representing the vibrational internal energy. When vibrational relaxation occurs, the energy distribution is changed as the system returns to a state of equilibrium. In order to model this behavior, the energy generated from the molecules vibrational degrees of freedom is treated separately from the energy generated from the translational and rotational degrees of freedom. We then write the total internal energy as
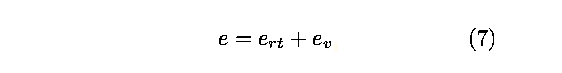
which represents the sum of the translational-rotational internal energy and the vibrational internal energy. In addition, the molecules are assumed to be linear harmonic oscillators so that the vibrational energy is given by, reference2,
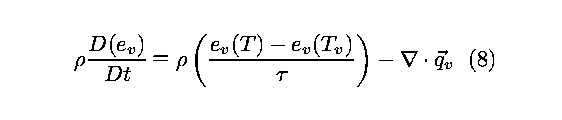
As with the internal energies, the specific heat can be written as a sum
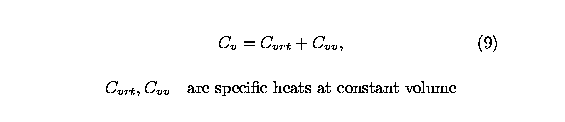
To obtain an equation for the translational-rotational energy we utilize the vibrational energy equation (8), and write the single-temperature energy equation (6) in terms of translational-rotational and vibrational components to obtain
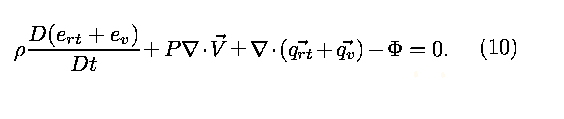
Subtracting equation (8) from equation (10) yields the translational- rotational energy equation 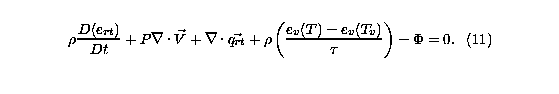Note that each energy is related to its respective temperature by a separate specific heat. For fully excited modes, each degree of freedom contributes RT/2 to the total energy, reference 4. Each diatomic molecule has three translational, two rotational, and one vibrational degree of freedom. Even for low temperatures, the translational and rotational modes are fully activated, so a good approximation to the rotational-translational specific heat at constant volume is 5R/2. The translational-rotational energy can then be expressed 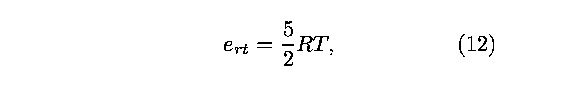where R is the ideal gas constant. The vibrational energy is found, reference2, to be 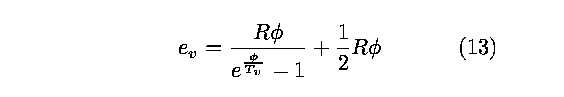This in turn produces the specific heat at constant volume for the vibrational mode as 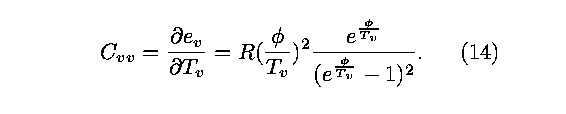The heat fluxes are also functions of temperature and are split into translational-rotational and vibrational components, so that 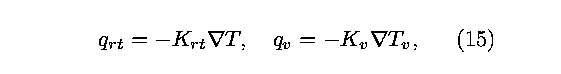The Prandtl number, Pr, is defined as 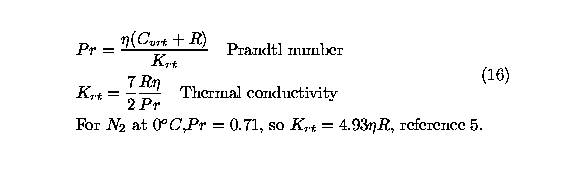The Schmidt number is defined as 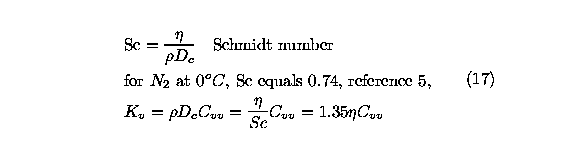This shows that the vibrational thermal conductivity is a function of both temperatures, since viscosity is a function of T and the specific heat is a function of the vibrational temperature.

For nitrogen, the relaxation time is taken from Meador, Williams and Miner, reference 3, and is calculated from

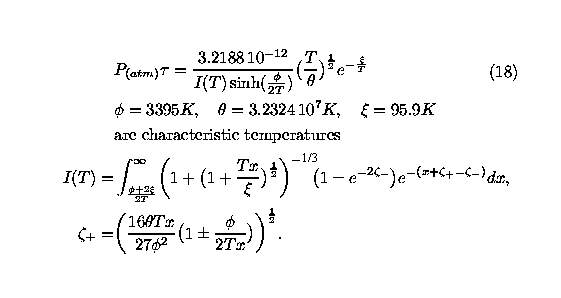
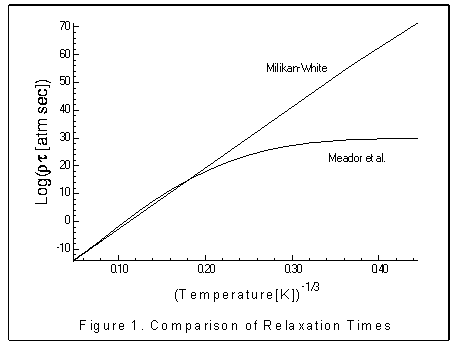
Figure 1 shows the relaxation time derived from equation (18) as it compares to the relaxation time developed by Millikan-White, reference7. Note the difference over the low temperature portion of the graph.

Governing equations for nonequilibrium case

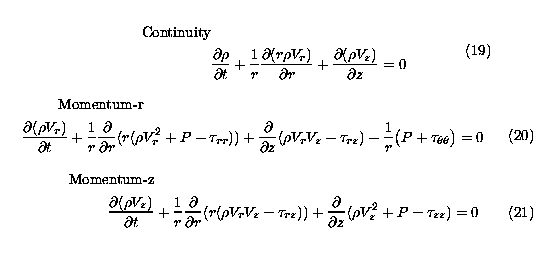
To summarize, in two dimensional axisymmetric coordinates, the equations which simulate the converging-diverging nozzle flow fields in the case of thermodynamical nonequilibrium are given by the following equations 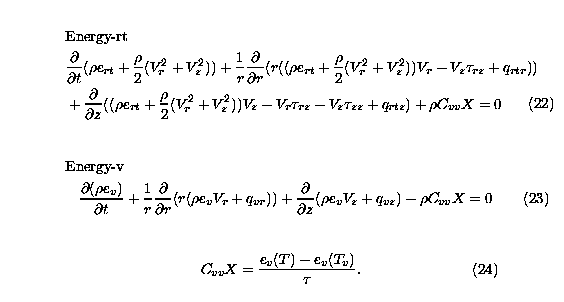The equations (19) through (24) are scaled by introducing the dimensionless variables defined by
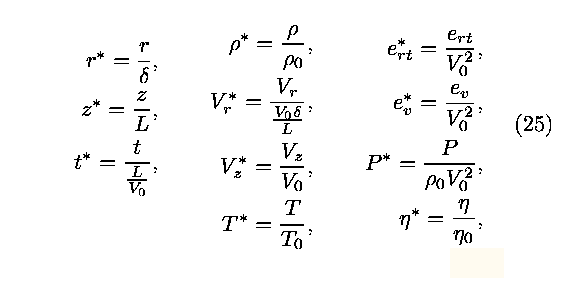
Finally, the nozzle is mapped to the computational domain by employing the change of variables,
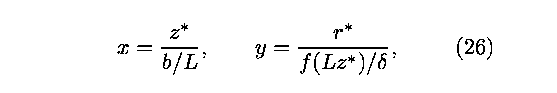
so that the nozzle is mapped to the unit square in the x,y plane. Consequently, the system of equations (19) through (24) are converted to the weak conservative form

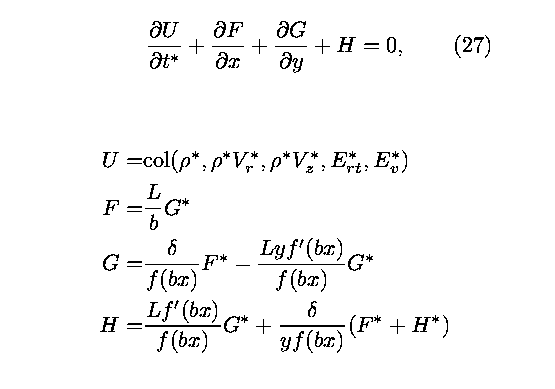
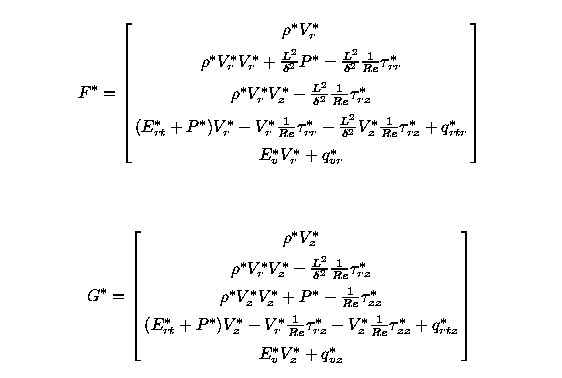
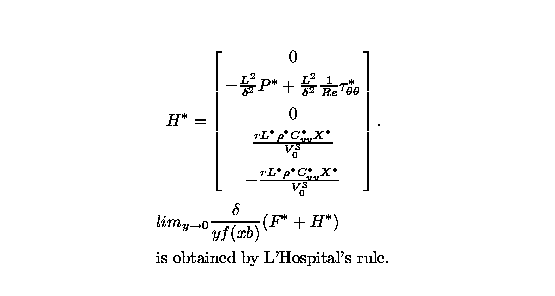
Boundary Conditions

The steady solution of the equations is uniquely defined by the boundary conditions. In order to obtain a meaningful solution, boundary conditions must be applied that are not only applied correctly but are physically meaningful, reference 8. The boundary conditions are expressed in terms of the primitive variables and are converted to scaled conservative variables when implemented numerically.

At the in flow boundary, the translational-rotational temperature is held fixed at some initial value. The vibrational temperature is assumed to be in equilibrium with the translational-rotational temperature at the inflow boundary and is also held constant at the inlet. In the computational coordinates, the gas is assumed to enter the nozzle parallel to the centerline, so the radial velocity is assumed to be zero. The axial velocity is held fixed at an initial velocity. Finally, to simulate subsonic inflow and supersonic outflow conditions, an analysis of the flow characteristics of Euler's equations suggests that one boundary condition must be left free to change with the solution of the interior flow, references 9,10. To this end, the density values are extrapolated from interior data. In the computational domain, this represents the condition that the partial derivative of the density with respect to distance is equated to zero. This is equivalent to the conditions

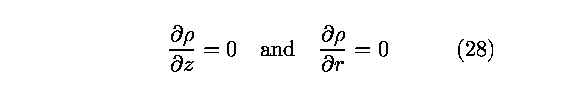
in the solution domain.

For supersonic flow, at the far-field boundary, all variables are extrapolated. From the relation

the pressure is also extrapolated.

The symmetry of the nozzle is used to specify the conditions on the center line. Assuming that the quantities above the center axis are mirrored by those below, the partial derivatives of the primative variables in the radial direction are equated to zero. Also along the center line we set the radial velocity to zero.

Lastly, boundary conditions on the nozzle wall are governed by the nozzle shape and the viscosity. On the nozzle surface we assume a no-slip boundary condition so that the radial and axial velocities are set equal to zero at the wall. Questions arose as to the correct translational-rotational and the vibrational temperatures at the nozzle boundary and so two scenerios are considered. The first case assumed that since the gas is not moving at the wall it is assumed to be in equilibrium. Thus, we used the boundary condition that

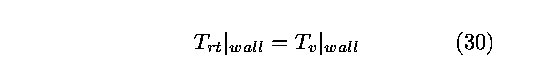
The second case considered both the translational-rotational and vibrationaltemperatures to be extrapolated at the wall. This produced the boundary conditions
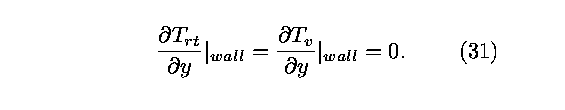
Following the recommendations given in reference 15, the pressure gradient normal to the wall is set equal to zero. The density on the boundary is then calculated using the ideal gas law evaluated on the boundary.

Initial Conditions

The choice of initial conditions is also important. Values that are too far from the steady solution can make the numerical solution unstable. Also, the closer the initial conditions are to the steady solution, the less time is required for convergence. To minimize the convergence time, we approximate the steady state solution with the steady solution of the corresponding one-dimensional inviscid problem. The flow is assumed to be in thermal equilibrium and isentropic. The one-dimensional values are then extrapolated and smoothed to match the boundary conditions. Further, in the computational coordinates the radial component of the input velocity was set equal to zero. For low pressure nitrogen gas flow a stagnation prssure of 50 psi and stagnation temperature of 3000K defined our simulation input parameters.

Numerical Methods and Results

The system of nonlinear partial differential equations given by equation (27) are discretized over a nonuniform grid which consists of n+1 rows and m+1 columns. We let
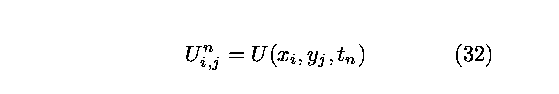
denote the solution at an interior grid point. The points in rows 0 and n or columns 0 and m are boundary points and are updated after each iteration. In the axial direction the grid is divided into four regions and in the radial direction it is divided into three regions. This forms twelve separately spaced regions, where the number of grid points in any region can be adjusted. The spacing between rows and columns varies to allow for a finer resolution near the throat and in the boundary layer. In general, the irregular grid spacing goes from fine to course in the axial direction and from course to fine in the radial direction.

The system of equations (27) was solved using the implicit method of Steger-Warming flux vector splitting described in reference 11. As a check on the results, the steady solution was also computed using the implicit MacCormack method described in reference 12. Both techniques used a 81 by 41 grid and gave consistent results. Details of the implementation of these methods are provided in reference 2.

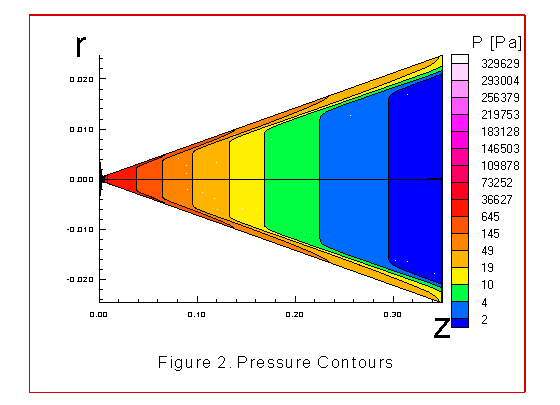
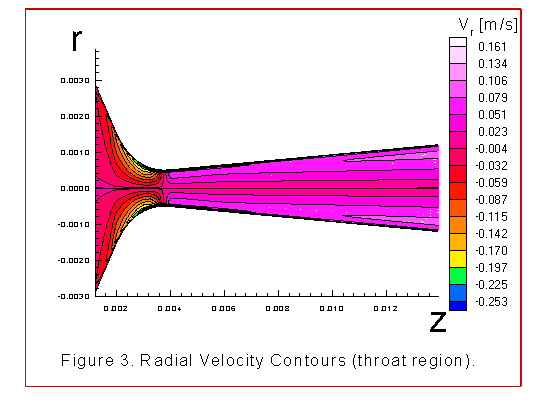
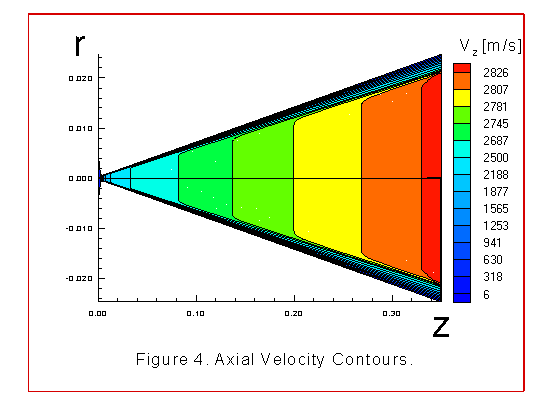
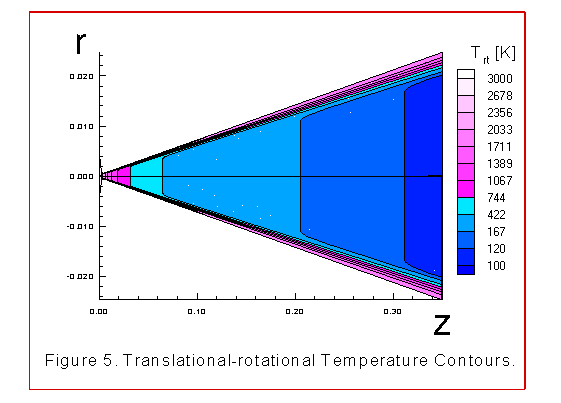
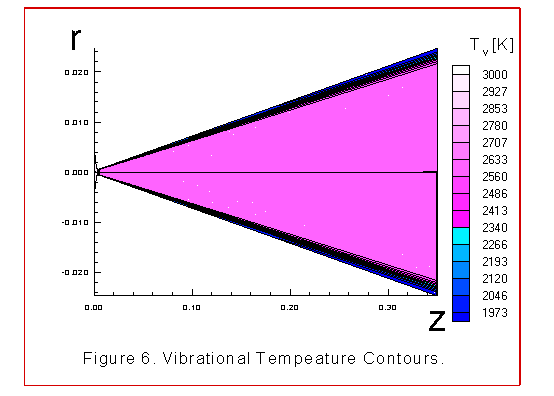
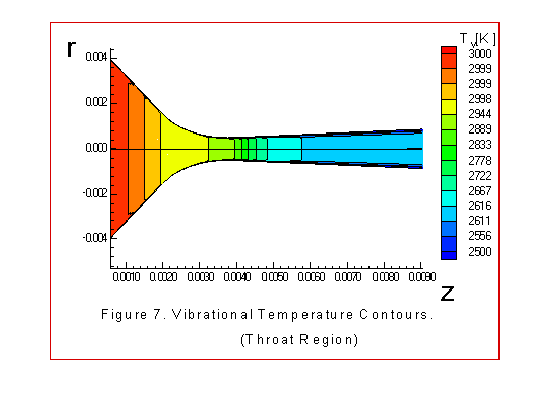
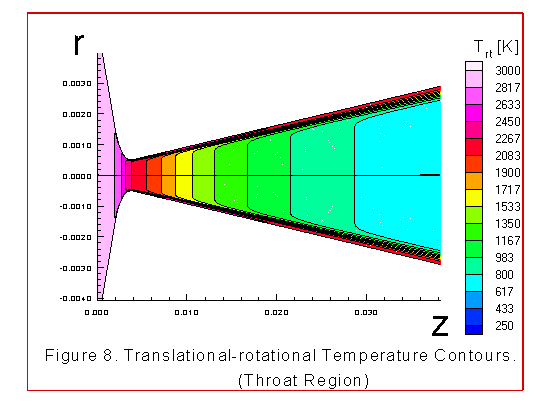
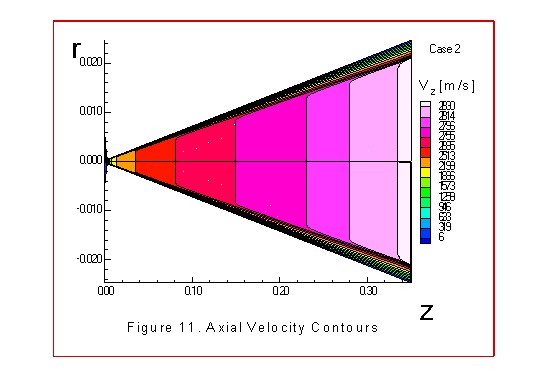
The figures 2 through 8 illustrate various contour plots of the numerical results describing the flow for case1, where the translational-rotational temperature was equated to the vibrational temperature at the wall. These figures give the pressure contours,radial velocity contours, axial velocity contours, translational-rotational temperature contours and vibrational temperature contours.

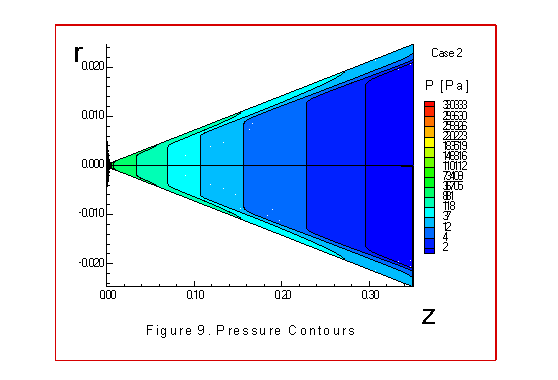
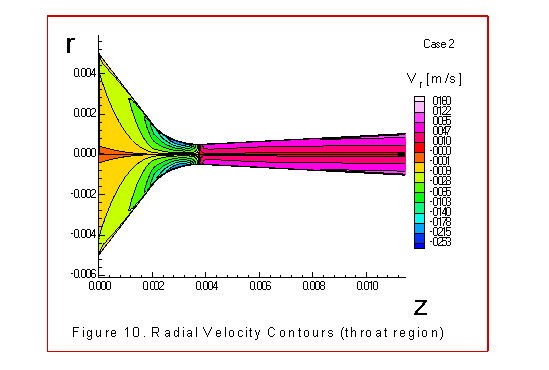
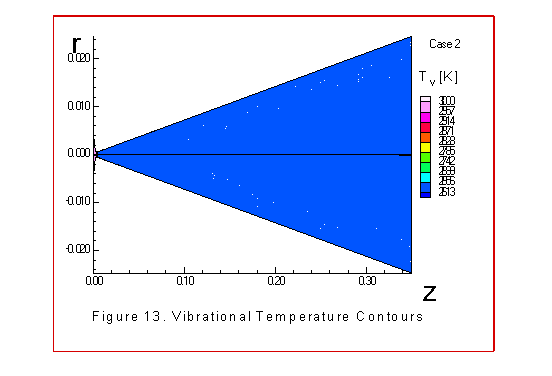
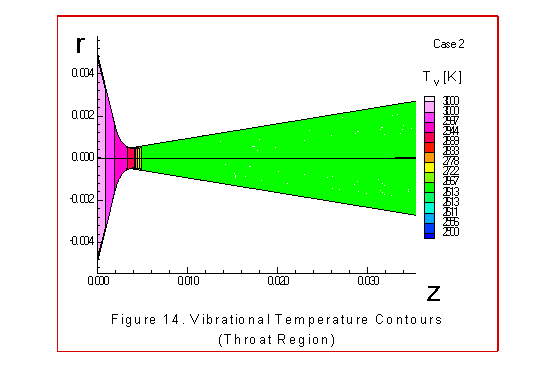
The figures 9 through 15 illustrate similar contours for the case 2, where both the translational-rotational temperature and vibrational temperature were extrapolated at the the wall boundary. We make the following observations concerning these graphs. Note that the pressure drop is large to insure that a shock wave does not occur between the throat and exit plane. The radial velocity contours match intuitive expectations. Usually these contours are not plotted as their values are several orders of magnitude less than the axial velocities. In both cases 1 and 2 the axial velocity contours increased from 6m/s to 2837m/s at the exit plane with uniform, almost linear contours in the diverging section of the nozzle. The size of the boundary layer is small as is expected. There is a big difference in the temperature contours. The translational-rotational energy experiences a large loss of energy as the gas expands through the throat. This temperature changes from 3000K at the entrance to 112K at the exit. These changes, along with the large pressure drop, suggested that maybe the continuum model was breaking down. A check on the Knudsen number showed that we were still within the range of a continuum model, reference5.

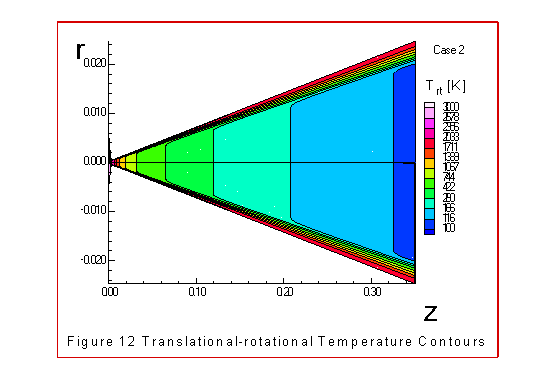
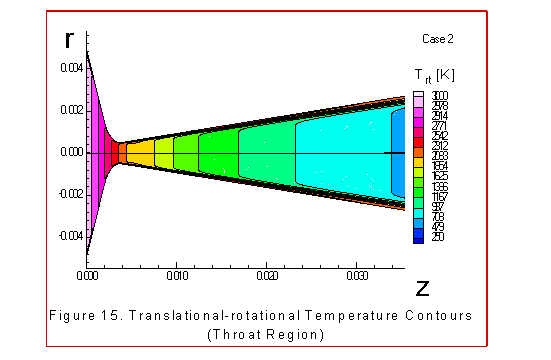
Boundary behavior is noticeable in figures 4, 5 and 6. Note that the rotational-translational temperature is increasing toward the wall. This can be explained by the energy equation (22) where for values of zero wall velocities we find

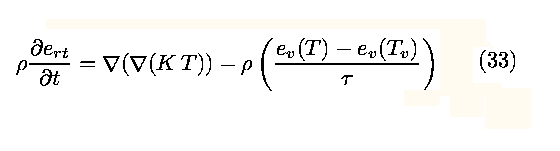
Observe that when the rotational-translational temperature is less than the vibrational temperature, then the difference in the last term of equation (33) is negative and so the coupling term increases the internal energy and therefore there is an increase in the translational-rotational temperature. Also as the gas nears the wall it slows and there is more time to relax with an increase in the vibrational to translational-rotational energy transfer. The most noticeable feature of the vibrational temperature contours is the freezing of the vibrational temperature, along the centerline, downstream of the throat. This is consistent with what other investigators have observed for their models, references 1, 13, 14. However, the2 flow is not in equilibrium before the throat,as suggested in reference 13, because the translational-rotational temperature drops much faster than the vibrational temperature in the converging section as illustrated in the figures 7 and 8.

In the diverging portion of the nozzle the vibrational temperature freezes while the translational-rotational temperature steadily decreases. Near the wall boundary and far down stream the translational-rotational temperature is increasing faster than the vibrational temperature is decreasing. This type of behavior may be one type of a driving force leading to turbulent motion. This can be seen in the radial velocity contours illustrated in figure 3.

In comparing the results from cases 1 and 2 we find that requiring equilibrium of temperatures at the wall produced some turbulent behavior which begins after the nozzle throat within the boundary layer region. Down stream of the throat the effect is less noticable. In addition, there were larger pressures at the inlet and wall boundary due to the extrapolated temperature boundary conditions.

Concluding Remarks

Other investigators have included vibrational nonequilibrium in their models of nozzle flow, references 1, 13, 14. Our modeling of vibrational nonequilibrium is consistent with that of the previous researchers with differences in boundary conditions, relaxation times and use of mach number. By comparison with other research,we have used an improved relaxation time over the temperature ranges considered. Our results indicate that the flow quality was good. We did not obtain the poor flow quality as found in reference 1, mainly because our nozzle shape was conical and was different than that of reference 1. Our numerical calculations were different also. The reference 1 states that they used the speed of sound and mach number extensively in their CFD algorithm. In our work we have not used the speed of sound or mach numbers anywhere in our calculations since mach numberis calculated from sound speed which is a function of sound frequency in nonequilibrium gas dynamics. This sound frequency is unknown so any use of mach number or sound speed could be misleading. Both of the numerical methods of Steger-Warming flux vector splitting and the implicit MacCormack method were used to check the validity of our numerical results. Both of these methods proved capable of handling the complexities of our modeling and gave consistent numerical results.

REFERENCES

1. Canupp P., Candler G., Perkins J., Erikson W., "Analysis of Hypersonic Nozzles Including Vibrational Nonequilibrium and Intermolecular Force Effects", 30th Aerospace Sciences Meeting, AIAA92-0330, January 1992.
2. Landry J. G., Nozzle Flow with Vibrational Nonequilibrium, Ph.D. Thesis, Old Dominion University, December 1995.
3. Meador W. E., Williams M D., Miner G. A., "Scaling of Vibrational Relaxation in Nitrogen Gases", (NASA Technical Report, in preparation).
4. Kauzmann W., Kinetic Theory of Gases, W. A. Benjamin, Inc., 1966.
5. Hirschfield J. O., Curtis C. F., Bird R. B., Molecular Theory of Gases and Solids, John Wiley and Sons, 1954.
6. Benedict R.P., Fundamentals of Gas Dynamics, John Wiley and Sons, Inc., 1983.
7. Millikan R.C., White D.R., "Systematics of Vibrational Relaxation", Journal of Chemical Physics, Vol. 39, No. 12, 3209-3213, December 1963.
8. Shang, J.S., "An Assessment of Numerical Solutions of the Compressible Navier-Stokes Equations", AIAA 17th Fluid Dynamics, Plasma Dynamics and Lasers Conference, AIAA 84-1549, June 1984.
9. Hoffman K.A., Chang S.T., Computational Fluid Dynamics for Engineers, Vol1. and Vol.2, Engineering Education System, Wichita, Kansas, 1993.
10. Thomas P.D., "Boundary Conditions for Implicit Solutions to the Compressible Navier-Stokes Equations in Finite Computational Domains", AIAA Computational Fluid Dynamics Conference, AIAA 79-1447, July, 1979, Williamsburg, Va.
11. Steger J.L., Warming R.F., "Flux Vector Splitting of the Inviscid Gasdynamic Equations with Applications to Finite-Difference Methods", Journal of Computational Physics 40, 263-293, 1981.
12. Anderson D.A., Tannehill J.C., Pletcher R.H., Computational Fluid Mechanics and Heat Transfer, Hemisphere Publishing Co., 1984.
13. Gnoffo P.A., "Application of Program Laura to Thermochemical nonequilibrium Flow through a nozzle", Hypersonic Flows for Reentry Problems, Vol.2, Springer-Verlag, 1145-1158, 1991.
14. GokÇen T ., "Computation of Nonequilibrium Viscous Flows in Arc-Jet Wind Tunnel Nozzles", 32nd Aerospace Sciences Meeting, AIAA-94-0254, Jan., 1994.
15. Yee H.C., Warming R.F., and Harten A., "Implicit total variation diminishing (TVD) schemes for steady state calculations, "J. Comput. Phys., 49, 377-393, 1983.