OLD DOMINION UNIVERSITY     DEPARTMENT OF MATHEMATICS AND STATISTICS

Numerical Analysis I - MATH 621 - Dr. Bogacki

Notes for Section 1.1 - Programming Suggestions

Contents

Programming and Coding Advice

Study all 18 items.

Many of the recommendations apply regardless of the programming environment, e.g.,

Others tend to apply to some environments only (such as FORTRAN). In particular, Mathcad has no integer type, no parameter statement, or arrays three- or higher-dimensional (although it allows for arrays inside of other arrays.)

Case Studies

The paragraphs on Exponents state that in many computing environments, the expression xy is computed as exp(y lnx).

One of the consequences of that is that an attempt to evaluate an expression like (- 8)1/3 will typically result in an error, as shown in the following FORTRAN example:

FORTRAN
code 
      REAL X,Y
      X=-8.0
      Y=1.0/3.0
      WRITE (*,*) 'The value of X**Y=',X**Y
      END
output
run-time error M6201: MATH
- **: DOMAIN error

Other important paragraphs in this subsection are these dealing with avoiding mixed mode, precision, limiting iterations, and floating point equality.

First Programming Experiment

Here is an implementation of the pseudocode from page 13 in FORTRAN:

FORTRAN
code 
      INTEGER N
      PARAMETER (N=10)
      INTEGER I
      REAL ERROR,H,X,Y
      X = 0.5
      H = 1.0
      DO 10 I=1,N
         H = 0.25 * H
         Y = (SIN(X+H) - SIN(X))/H
         ERROR = ABS(COS(X) - Y)
         WRITE (*,*) I,H,Y,ERROR
   10 CONTINUE
      END
output 
          1    2.500000E-01    8.088529E-01    6.872965E-02
          2    6.250000E-02    8.620341E-01    1.554842E-02
          3    1.562500E-02    8.738014E-01    3.781152E-03
          4    3.906250E-03    8.766440E-01    9.386062E-04
          5    9.765625E-04    8.773483E-01    2.342581E-04
          6    2.441406E-04    8.775240E-01    5.854360E-05
          7    6.103516E-05    8.775679E-01    1.461498E-05
          8    1.525879E-05    8.775789E-01    3.647725E-06
          9    3.814697E-06    8.775817E-01    9.059112E-07
         10    9.536743E-07    8.775823E-01    2.502601E-07

The same pseudocode implemented in Mathcad:

Mathcad
code
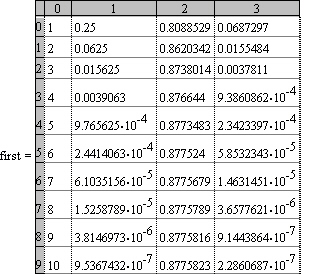
output
(The Mathcad source can be found here.)

Note the difference between the values from the two implementations. The difference can be attributed to Mathcad's numbers being implemented as 64-bit floating point numbers, just like FORTRAN's DOUBLE PRECISION numbers on IBM-PC-compatibles.

If in the FORTRAN code above, we change REAL to DOUBLE PRECISION, then similar output will result.