Paul Bouthellier
Department of
Mathematics and Computer Science
University of
Pittsburgh-Titusville
Titusville, PA
16354
FAX: 814-827-5574
PH: 814-827-4432
E-mail: pbouthe@pitt.edu
The first two applications we consider make use of GSPís ability to paste images under a grid. The first example pastes a curve into GSP and plots points on the curve to get coordinate pairs. These coordinate pairs are then used to create an interpolation polynomial using Maple. The interpolation polynomial is then used in a web page allowing people to enter x-values and get out estimates of the corresponding y-values of the original graph. The second application pastes a 2-dimension image of some object; say a car or motorcycle, into GSP. Using GSP we then break the object up into a series of points and circles. The points will be used to model straight lines and polygons. These elements can then be used with Java to create models of the original objects on web pages. These projects teach students about mathematical modeling.
The final application we look at is that of morphing. Using GSP we can illustrate the general principals of morphing for simple objects, for example, how a square can be morphed into a circle. Theory can be then turned into practice using the package Flash-which does excellent 2-dimensional morphing for simple objects. GSP can then be used to study how an object such as a spiral can be morphed into a circle. Flash again can be used to illustrate the theory. The concepts of morphing can then be generalized to 3-dimensional space and illustrated for simple objects-such as spheres and cubes using Amophium 3.
I) Using GSP for Interpolation
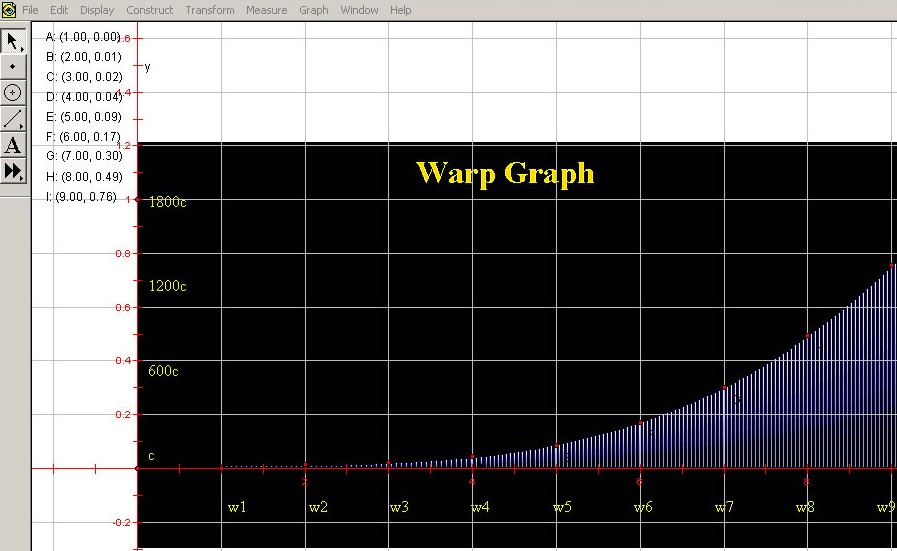
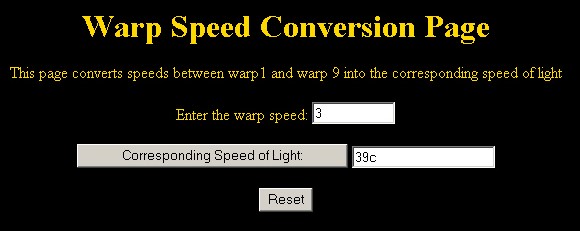
The first problem we looked at is that of curve fitting. GSP allows students to paste an image of a graph and to plot points on the graph that can be used for interpolation. One example we looked at was fitting a 8th degree polynomial through a curve which related warp speed to the corresponding speed of light in the Star Trek universe. As can be seen in the following graph, 9 points were placed on the graph, corresponding to warps 1 through 9. The coordinates of the labeled points are then derived. (Settings in GSP allow for more decimal places if required.)

It will be noted that the students have to scale the y-values between the scale used in GSP and the original graph. (Axes can be scaled in GSP but getting an exact fit can be rather difficult.) The 9 points, labeled A through I, can then be used to compute an interpolation polynomial using a package such as Maple. The resulting interpolation polynomial can then be programmed as a web page using a language such as JavaScript. The result is a calculator that can be used to approximate the original graph.
Many such graphs can be used: population growth, Internet growth, approximating the area under a curve using an interpolation polynomial etc....
II) Mathematical Modeling
Two dimensional geometric objects can often be modeled using lines, rectangles, circles, and triangles. These basic geometric objects, and their equations, can be created in GSP. One simple example is given by a no-smoking sign-which is modeled in GSP.
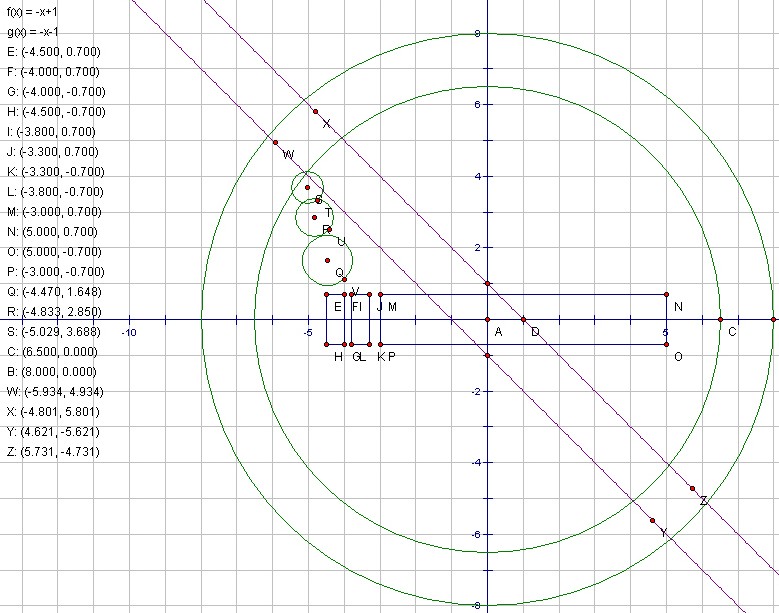
Using the equations of the circles and the points which make up the rectangular shapes in the object, a mathematical model using ActiveX or Java can be used to create a model of the no-smoking sign which may be put on the web. An example using Java is given below:

When modeling objects it is often best to allow students to choose an object they wish to model. Examples of past projects have been: no-smoking signs, a globe, a motorcycle, the interior of a room, and a map of the United States.
III) Illustrating the Basics of Morphing
Using GSP one is able to show how points on a circle may be mapped to points on a square interactively using GSP as illustrated in the following image:
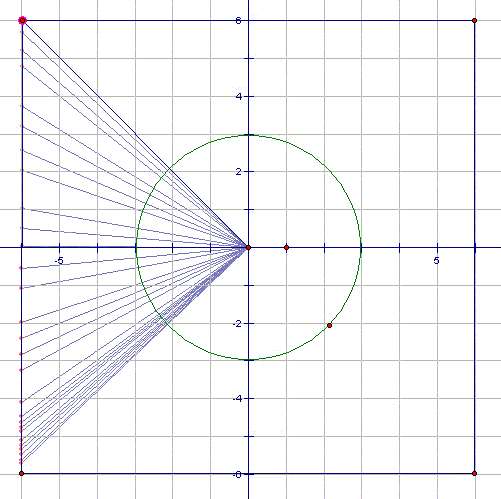
In lower-level classes the basic concept of a one-to-one mapping can be used to describe the basic ideas of morphing. In classes in trig and beyond the actual equations can be derived. Using the shape-tweening feature of Flash one is able to create an animation showing the morphing of a circle to a square. A series of frames from such an animation is shown below.

In more advanced classes the concept of morphing can be generalized to non one-to-one functions and to 3-dimensional objects (calculus III and beyond).
|
|
|
|
Spiral to Circle (Flash MX 2004 Pro) |
Sphere to Cube (Amorphium 3) |
IV) Conclusions
GSP allows for the construction of points, lines, circles, and polygons that can be used in concert with other packages to study a wide range of problems. One other problem that GSP is useful for is that of illustrating the concept of collision detection (as illustrated below).