Paul Bouthellier
Department of
Mathematics and Computer Science
University of
Pittsburgh-Titusville
Titusville, PA
16354
FAX: 814-827-5574
PH: 814-827-4432
E-mail: pbouthe@pitt.edu
Collision theory can be used to study topics from high-energy collisions between particles in particle physics to creating a billiard simulator on a computer or a gaming console. Depending on the assumptions made, the treatment can be quite simple or quite complex. Basic assumptions will be made about the properties of collisions to make the results realistic. Allowing students to choose the size and shape of the boundary of the “pool table” on which the collisions take place allows students a good deal of control in how the final results will look and establishes some of the equations which must be solved.
It is quite easy to illustrate the collision problem, as most people are familiar with pool-even if they have not played it. I show one version of a completed program that runs at a slow enough speed to allow students to see the effects of collisions. We then discuss the basic assumptions that we make and show that they are reasonable. The software package Geometer’s Sketchpad is also useful to illustrate the concepts.
After the students decide on the size and shape of the table they want, and the basic assumptions on the collisions are made, the students solve the equations. Their results are then programmed in JavaScript. Before we begin, I show the code of several similar programs to illustrate the basic syntax of the language. We then, as a class, construct the program and run the results as a web page. If the simulation does not behave as expected, the students recheck their results, make corrections as necessary, and run another simulation.
I) Basic equations of collision theory
We shall study the case of several dozen objects of equal mass in motion within a fixed two-dimensional enclosure. To study the effects of collisions between these objects we first look at the collision of just two objects as follows:

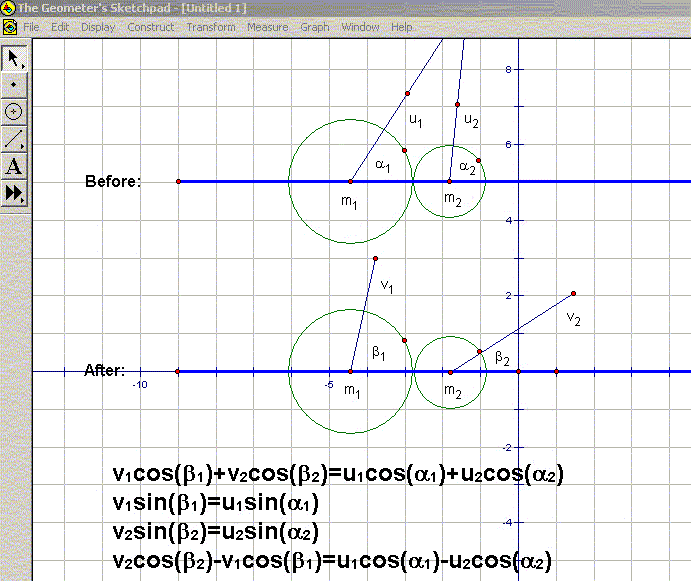
Figure 1
m1 and m2 are the masses, u1 and u2 are the initial velocities, α1 and α2 are the initial angles made with the line through the centers; v1 and v2 are the resulting velocities and β1 and β2 the resulting angles (with respect to the original center line) [1]. For simplicity we shall assume that the masses of the objects are equal.
The equations in Figure 1 relate the angles and velocities or the objects before and after collision. These equations assume, for the sake of simplicity; perfect elasticity and that there are no external forces along the lines of centers [1]. It will be noted that we are not taking into account friction due to the surface of the table, the cushion of the table, the material of the spheres, effects of chalk, temperature, air pressure, etc...
To illustrate the effects of collisions between two objects: a handy pool table is perfect, a tape from a pool tournament (shown on ESPN) if the pool table is not available, collide two coins, or use Geometer's Sketchpad to illustrate (via traces) the before and after trajectories of the objects.
II) Layers and Trigonometry
To introduce students to the concept of layers in JavaScript, I created a simple program which showed a group of objects radiating outwards from the center of the screen.

Figure 2
The code is given as follows:
<html>
<head>
<title>layers</title>
<script language="JavaScript">
var msg="***********************************************";
var arraystring=msg.split('');
var n=msg.length;
var xpos=new Array();
var ypos=new Array();
var xmov=new Array();
var ymov=new Array();
var ht=screen.availHeight;
var wd=screen.availWidth;
var trigger=0;
var hits=0;
var totalspeed=0;
var programspeed=0;
var coll=new Array();
for (var i=0;i<n;i++) {
coll[i]=new Array();}
for (var i=0;i<n;i++) {
for (var j=0;j<n;j++) {
coll[i][j]=0;}}
for (var i=0;i<n;i++) {
xpos[i]=wd/2-30;
xmov[i]=Math.cos(Math.PI*2/parseFloat(n)*i);
ymov[i]=-Math.sin(Math.PI*2/parseFloat(n)*i);}
for (var i=0;i<n;i++) {
document.write('<div id="Layer"
style="position:absolute;left:0px;top:0px;width:40px;height:40px">' + '<span
style="color:#ffd700;font-size:40px">' + arraystring[i] + '</span>' + '</div>');
}
function move() {
for (var i=0;i<n;i++) {
totalspeed=0;
xpos[i]+=xmov[i];
ypos[i]+=ymov[i];
Layer[i].style.pixelLeft=Math.round(xpos[i]);
Layer[i].style.pixelTop=Math.round(ypos[i]);}
Note only does this illustrate the concept of layers but also illustrates another use for trigonometric functions.
III) Bouncing off the Sides
Allowing the students to choose the shape of the "table" on which the objects exist within allows students some say on how the final results will look. Some possible shapes for the table are given below:
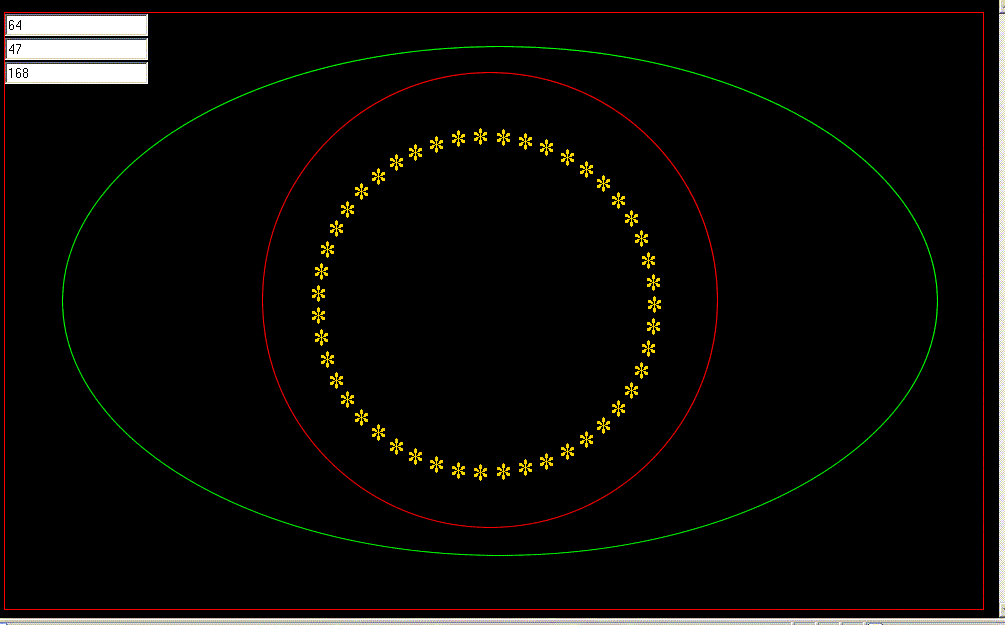
Figure 3
Using a non-rectangular table means students need to find the slope at each point along the edge of the table in order to compute trajectories after an object collides with the boundary of the table.
IV) Solving the Equations
Given the initial velocities u1 and u2 and angles α1 and α2 of two colliding objects, the goal is to solve for the resulting velocities v1 and v2 and angles β1 and β2 in terms of the original parameters. As we wish to implement our solutions as a JavaScript program we need to taken into account that all angles given are relative to the line of centers. Hence we also will need to rotate our solution through an angle φ to program the results in standard xy-coordinates. Where (x1, y1) and (x2, y2) are the centers of the masses m1 and m2 respectively (refer to Figure 1):
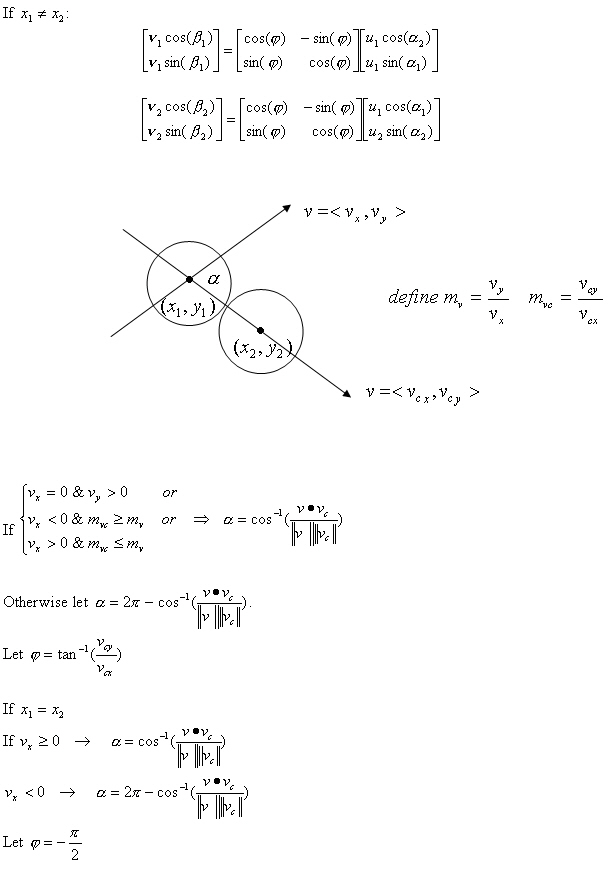
This algorithm can now be programmed into JavaScript. (In JavaScript the y-coordinates increase downwards so this must be taken into account in the program.)

There are a number of related problems that can be studied :
V) Conclusions
The collision problem can be studied at levels from trigonometry to advanced mathematics courses. By turning the solutions into a program students can see their equations "come to life".
References
[1] Chapter 5 Collisions by Dr. J. B. Tatum, University of Victoria British Columbia.