Interactive Calculus Laboratories Using Maple V

 

Shari Prevost
Department of Mathematics and Computer Science
Gainesville College
Gainesville, GA 30503
Phone: (770) 718-3807
E-mail: sprevost@hermes.gc.peachnet.edu
 
Abstract
The use of interactive Maple worksheets in the calculus curriculum can make abstract concepts such as the definition of limit or iterative processes like Newton's Method come alive. This paper will exhibit some examples of such activities.
  1. Introduction

    2. During the previous academic year a number of the faculty in the Mathematics and Computer Science Department at Gainesville College have added a laboratory component to their calculus courses. The majority of these laboratories are interactive Maple worksheets that are designed to engage students in mathematical explorations that will help them obtain a more profound understanding of the mathematical concepts they encounter. Whether the topic is the epsilon-delta definition of limit, Newton's Method, volumes of solids of revolution, or limits of sequences, Maple can provide a valuable graphical and computational tool that allows the student to more thoroughly investigate each of these mathematical notions. In this paper I will describe the laboratories and give a few examples of the mathematical explorations that take place in the laboratories.
     

  2. Description of the Maple Laboratories

    3. As mentioned above, the laboratories are interactive Maple worksheets. These worksheets are found on line and can be accessed at any computer on campus. The class will meet for 50 minutes in a room that is designed for a computer-based laboratory. The physical set up of the computer room encourages teamwork. There are fifteen Pentium processor PC's which are spread out along the outer walls and in a small cluster in the middle of the room. The students are encouraged to work in teams of two or three. This is easily accomplished since the class size is usually between 25 and 30 students.

    Each laboratory is designed to provide an opportunity for mathematical exploration and discovery, produce graphical and numerical evidence to support the mathematical notions presented, foster collaborative learning, and make the computer algebra system Maple as friendly as possible. In order to produce Maple friendly labs, many new Maple procedures have been written. For example, the laboratory that discusses Newton's Method introduces two local Maple commands: NewtonsMethodTable and NewtonsMethodPlot. NewtonsMethodTable produces a table that displays the (numeric) results of the iterative process, while NewtonsMethodPlot displays the iterative process graphically.

    The students are not expected to complete the assignment in the 50-minute lab period. However most students finish approximately one half to one third of the material during the class lab period. The students are given one week to complete the laboratory and turn in a laboratory report. Since the Maple worksheets can be accessed on any computer on campus, there is adequate time and computer availability for students to complete the laboratory assignment.
     

  3. Examples

    4. Many of the laboratories focus on the theory behind the formulas and techniques that students learn in calculus. Maple provides an excellent environment to explore the meaning of the epsilon-delta definition of limit or the definition of limit of a sequence, or to "visualize" the iterative process known as Newton's Method.

    In the laboratory entitled, "Exploring Limits," the students are presented first with an intuitive definition of the limit of a function as the input approaches a single number. They are then asked to evaluate a set of limits based on graphical evidence and then numerical evidence. The graphical evidence is gathered using the Maple command plot, while the numerical evidence is obtained with the locally written Maple procedure LimitTable. A template for LimitTable follows:

    LimitTable(f(x),x=a,left);
    creates a table which calculates f(x) for x=a-.1,a-.01, ... , a-10^(-10), and
    LimitTable(f(x),x=a,right);
    creates a table which calculates f(x) for x=a+.1,a+.01, ..., a+10^(10).
    To gather numerical data for the limit as x approaches 2 from the right of the function  we can use the Maple command LimitTable. We need to open an evaluation cell, type the input LimitTable(x^2,x=2,right); and evaluate. Maple would then return

    From the numerical data provided by LimitTable, students conclude the limit of f as x approaches 2 from the right is 4.
     
    The last section of this laboratory focuses on the e-d definition of limit. Here the students explore how to satisfy the definition of limit for a given function as x approaches a point a and a specified e value. The Maple command utilized is LimitPlot. The template for LimitPlot follows:

    LimitPlot(f(x),x=b..c,a,L,epsilon);
    plots the graph of y = f(x), and the lines y = L-e, y = L, and y = L+e over the x-range
    [b , c], and shades the region L-e< y <L+e, and
    LimitPlot(f(x),x=b..c,a,L,epsilon,delta);
    plots the function y = f(x) in black on the intervals x £ a-d and x ³ a+d and in red on the interval a-d< x < a+d, the lines y = L-e, y = L, and y = L+e, and shades the region L-e < y < L+e.
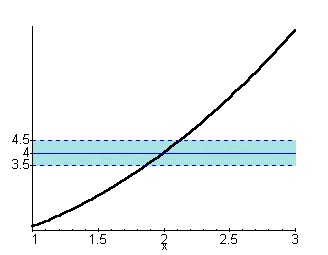
    Let's once again consider . In the previous sections the students have gathered enough graphical and numerical evidence to convince them the limit is 4. We can now ask the students to find a d that will satisfy the definition of limit for the function , the limit point 2 and an e value of 0.5. To get an idea of the behavior of the function near 2, the student is instructed to first evaluate the Maple input LimitPlot(x^2,x=1..3,2,4,.5); The Maple output is given below.

    A quick inspection of the graph looks like d=0.2 may satisfy the definition of limit for e=0.5. To check this the student is asked to evaluate the Maple input LimitPlot(x^2,x=1..3,2,4,.5,.2); The Maple output which results is seen below.

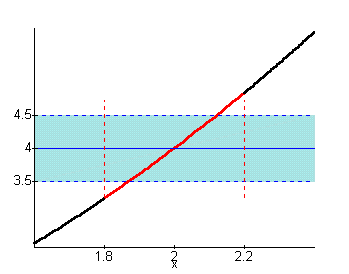
    It is easily seen that the red portion of the graph is partly outside the shaded region, and hence the choice for d doesn't work. It is too large. So the student is instructed to try a smaller one. The input LimitPlot(x^2,x=1..3,2,4,.5,.1); is evaluated and gives the output

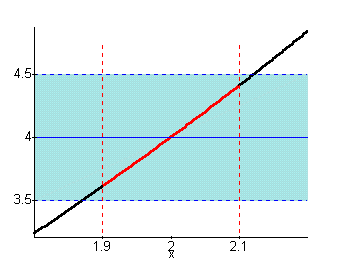
    The lab continues by asking questions about how the value of d changes as e changes for a given function and limit point. The students are also asked to repeat the above exercises for a few other functions.

    The laboratory entitled "Linearization and Newton's Method," describes the process of the linearization of a differentiable function near a point, and then discusses an important application of linearization, namely Newton's Method. Maple can be used here to provide quick numerical results and display the iteration process of Newton's Method graphically. The Maple tools created to give the numeric and graphical assistance are NewtonsMethodTable and NewtonsMethodPlot. The templates for these procedures follow.

    NewtonsMethodTable(f(x),x=a,n=N);
    produces a table with the first N terms in the Newton's Method iterative process beginning with x[1]=a,
    and
    NewtonsMethodPlot(f(x),x=1,n=N);
    provides an animation which depicts the Newton's Method process through the first N terms.

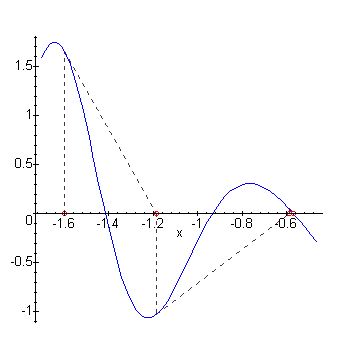
    In the Newton's Method laboratory we use Newton's Method to find the roots of the function . The student can get the numerical information of Newton's Method quickly using NewtonsMethodTable and then can see the process graphically by using NewtonsMethodPlot. For example, the Maple input NewtonsMethodTable(sin(3*x^2)-sqrt(x^2+1)+x^2,x=-1.6,n=10); produces the table

    The Maple input NewtonsMethodPlot(sin(3*x^2)-sqrt(x^2+1)+x^2,x=-1.6,n=8); gives the graphic
    This graphic output is actually an animation.  The animation takes the viewer along the path of the iteration: from initial point, to the point on the graph associated to it, to the place the tangent line to the graph intersects the x-axis, and so on.
     
     
  4. Conclusion

    5.  
    The wonderful graphic and computational abilities of Maple can be utilized to create interactive discovery-based activities that promote a more profound understanding of the mathematical ideas found in a typical calculus course.  The topics can range from the more abstract ideas of limits and convergence to more applied topics such as Newton's Method.
     
  5. References
    1. Heck, Andre. Introduction to Maple. Springer-Verlag, second edition, 1996.
    2. Prevost, Shari. Exploring the e-d Definition of Limit with Mathematica. Mathematica in Education, volume 3, no. 4, 17-21, 1994.