LUA, Seu-Kea
WONG, Wai-Har Selina
Ngee Ann Polytechnic
Singapore
535, Clementi Road, Singapore 599489
Emails : lsk1@np.ac.sg / wwh1@np.ac.sg
Abstract
This is an example showing how Scientific Workplace is used as an effective tool to do live mathematics and to prepare report. A portion of an Extended Exercise which involves solving a definite integral is used. The existing feature of function definition in the system is manipulated to perform trapezoidal rule.
Introduction
In the experience of teaching mathematics to a group of engineering students, the author has been administering extended exercises to the students as part of their assessment to supplement the traditional examination. Each of these exercises are given to students in the course of study and they are given about two to three weeks to solve one exercise. At the end a report must be submitted. These reports are then graded by the author and the grades contribute to the students final grade of the semester. It is believed that these extended exercises, when used properly, improve the learning of mathematics. These extended exercises, ideally, should begin with asking students to perform well defined tasks. From these rather 'closed' beginnings, the tasks becomes some unstructured problems or open-ended tasks that students can tackle in any way they choose. The context can be a real life problem, a puzzle or a mathematical proof. A well designed extended exercise provides students with opportunities to consolidate and practise fundamental skills and routines. It trains them in problem solving including application of mathematics to everyday situations and, especially, to their own field of study. It can also involve students in investigational work. Each of these is considered essential elements in mathematics learning.
In solving the extended exercise students are required to prepare a mathematical report which includes suitable headings and sections, appropriate explanations, calculations, tables or graphs, and any other relevant information. In the past, most students prepared hand written reports. Only a small proportion of them used a word processor to prepare the report, and they preferred to use scientific calculators to handle the calculations even when tedious and laborious arithmetic is involved. Although students were encouraged to use graphic calculators or to write their own computer program to solve problems, they did not see it as worthwhile nor a superior way in handling these extended exercises. As a result, some extended exercises, where too much calculation is involved, become quite impossible hence a burden to them . For example, a problem that involves evaluation of definite integral using trapezoidal rule with a large number of intervals, when given to students, became tedious to them. Scientific WorkPlace, however, made the problem solving and report writing very much easier and interesting.
The following is the solution of a section of an extended exercise prepared using Scientific WorkPlace. This particular exercise is suitable for students who are learning numerical integration.
Performing Trapezoidal rule using Scientific WorkPlace
In many practical problems the functions that have to be integrated are often difficult, or impossible, by analytical method. In this case, numerical method can be used to approximate the integral. As it is often known in advance in many engineering and scientific problems that the value of an integral is only required to a certain precision, numerical method, when used properly, is realistic and it can avoid considerable unwanted labor. Here we want to look at how trapezoidal rule can be used economically to evaluated definite integral.
Using trapezoidal rule to approximate the area under a curve involves
slicing up the area to be found into a number of strips of equal width,
approximating the area of each strip by the area of the trapezium formed
when the upper end is replaced by a chord; the sum of these approximations
then gives the final numerical result of the area under the curve. We
consider a definite integral 
. The points of
subdivision of the domain of the integration 
are
labelled x0, x1,... xn where x0=a, xn=b, 
, 
and the width of each strip is 
. The values of the integrand 
at these points are
denoted by 
. With this we have the trapezoidal
rule: 
We will now evaluate the integral 
using trapezoidal
rule and repeat the process for n=1, 2, 4, 8, 16. To do this we,
first of all, define the integrand 
. The procedure of
trapezoidal rule can be defined as the function 
where 
Here, a and b are the lower and upper limits of the integration
respectively. approximates the definite integral using trapezoidal rule with n num
ber of
intervals, provided is defined and that it is continuous
in the domain . As we have already defined 
, The approximated values of , with n=1, 2, 4, 8, 16, are given as follows:
As we know, when the number of intervals n increases the approximation of improves. It must be noted here that when using a
scientific calculator to solve this problem, the points at which the value
of integrand are to be calculated is one more than the number of intervals n . Although we can use the formula 
to work out the approximation each time, based on the
previous
approximation, when we do interval-halving. the calculation will still be
laborious as n increases. With defined function ,
however, we can quite freely increase the value of n and the Scientific
WorkPlace calculates the approximation of without much
of our effort.
Refer to the values of listed above and watch how
the approximations approaching the value of the integral obtained by
analytical method: 
. It
shows that the trapezoidal rule approximation is now accurate up to 3
decimal places. In general, of course, we do not know how good an
approximation this value is, and the usual practice is to continue
interval-halving until two successive extrapolated values agree to the
accuracy required.
In a situation where the students are unfamiliar with the analysis of error
bound, and yet, If it is of our interest to estimate the number of n such
that a certain degree of accuracy is to be achieved, the following method
can be used. We can define a function 
such that 
. The list of is obtained:
It should be clear that we expect 
. Therefore, 
The next task is to estimate how many intervals do we need to achieve a certain accuracy for the approximated integral.
Look at the next list of values:
It is seen here that is reduced to about 25% each
time when the number of intervals n is doubled. If we require 
to be accurate up to 5 decimal places, the error
should be given by 
. Using n=16
as a reference point, we can calculate a value k for which: 
.
This implies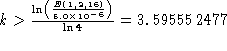 
. Choose the smallest integer value
of k such that k>3.6, i.e. k=4. This means 4 more times of interval
halving, when n=16, is required, or n=256, such that 
up to 5 decimal places.
Therefore, 
gives the approximation that is
accurate up to 5 decimal places. We can verify this claim by obtaining the
following approximation:
(accurate up to 4 decimal places)
(accurate up to 5 decimal
places)
In fact it is possible to obtain a new approximation for
by Richardson extrapolation. In any case, if we take 
, we obtain another approximation
better than 
for the integral. To perform the
extrapolation, we define the function 
.
The approximations obtained from Richardson extrapolation is listed as follows:
It can be seen here that by using the extrapolation the required accuracy is achieved quickly.
We can also look at the rate at which the computational error is reducing in
Richardson extrapolation. Define the function 
and obtain the
ratios 
as shown:
So, when using Richardson extrapolation, the computational error is reduced to about 6% each time when the number of intervals is doubled.
Conclusion
The amount of calculation in doing trapezoidal rule is tremendous. It is, however, not so when Scientific WorkPlace is used. When the laborious calculation is removed it becomes possible for students to investigate the effectiveness of the use of trapezoidal rule in evaluating different definite integrals. The scope of the problem can also be expanded, for example, to include the comparison of the characteristics of different integrands that affects the rate of convergence of the approximated value to the exact value of the definite integral. The content can also be organized for students self-learning, or for use as lecture material. As document created by Scientific WorkPlace can easily be sent electronically, it will make distance-learning very convenient.
If our students are to use Scientific WorkPlace effectively, they need to be trained and made familiar with the basic computing skill. Although not essential, knowledge in computer programming would definitely be an advantage. For example, to define a function that would perform trapezoidal rule like what was shown, though appears simple, is not straightforward, and requires much thought. Also, Students need to be convinced that, in the long run, this is a more superior tool to do mathematics with. In the process of using this system, teething problems can be expected. They can, however, be overcome. If the Scientific WorkPlace is to be used successfully for teaching purpose, it will demand more time and effort of the teachers at the initial stage. Teaching material will need to be arranged in such a way that it is possible for learners to do investigation, etc, as a follow up activity when the teaching is over.
We would like to thank Prof Yang, Wei-Chi at Radford University, Virginia, for his kind advice and suggestions in writing this paper. We would like to acknowledge that the example used was obtained from the book, Modern Engineering Mathematics, by G. James, published by Addison-Wesley Publishing Company.