While working on this activity students would work with Mathcad to perform calculations, generate 2D plots and record their answers. Several times during this activity, students would access a Maple template which will enable them to see the animation of the "roller" with a given radius "painting" the surface.
Note that the "roller" analogy will hold for any differentiable curve y=f(x), but will NOT hold for a general parametric curve (x(t),y(t)).
Here's the introduction to the activity
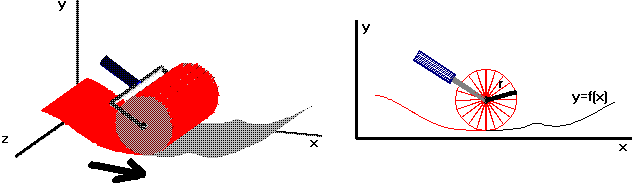
Consider a cylindrical surface whose generators are parallel to the z axis. Suppose the trace of the surface in the xy-plane is described by a given function y=f(x).
Your problem is to determine the largest radius of the roller which can be used to completely paint both sides of the surface. (We assume the axle of the roller is parallel to the z axis.)

Equivalently, your problem can be rephrased as follows: Find a circle with as big a radius r as possible which can be rolled over the upper and lower sides of y=f(x) while touching every point of the curve.
The particular curve to be painted in this problem is given by f(x)=sin(pi*cos(x/2)) for x in [0,5].
Students are now asked to watch animations of rollers attempting
to paint both sides of the given function. (Note that in these
animations, layers of paint have been artificially elevated to
make it easier to distinguish "painted" and "unpainted" portions
of the curve.)
The first animation corresponds to the radius=1
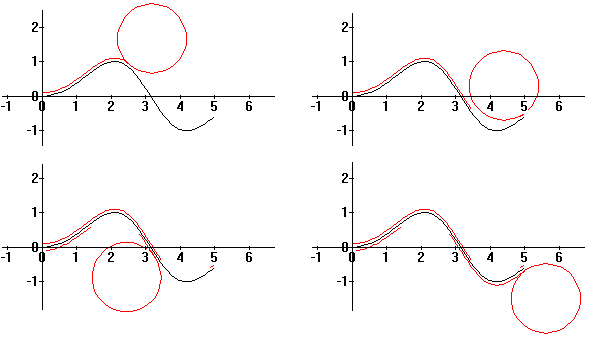
... and is obviously unsuccessful. The students then try r=0.4
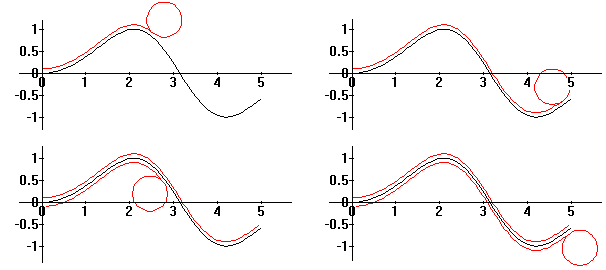
... and watch it succeed.
Students are then encouraged to experiment with different r values (between 0.4 and 1), but it becomes clear that this "trial and error" approach is not satisfactory.
At that point, Mathcad is used to plot the curvature of the curve, and students are asked to numerically find the maximum curvature value.
Finally, students are asked to generate two more animations: one with the radius of the roller taken to be the reciprocal of the maximum curvature they found; the other one with a slightly larger radius.