Limits
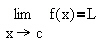
Two examples are illustrated:
|
|
Contents |
Limits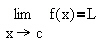 Two examples are illustrated:
|
 |
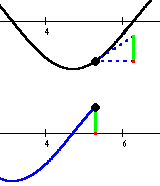 |
Slope vs. DerivativeNote that the positive rise/run values are indicated in green; negative values are indicated in red. This animation can be viewed for the following functions:
|
Arc LengthThe first example illustrates a sequence of polygonal approximations of a rectifiable curve, i.e., a curve with a finite arc length. In the second example, the curve has infinite length.
|
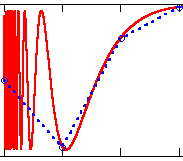 |
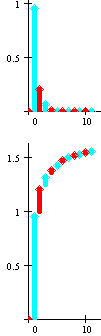 |
Infinite SeriesCurrently, animations corresponding to the following p-series are available:
|
Conic Sections |
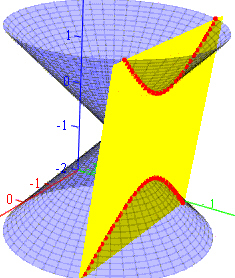 |
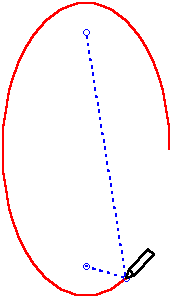 |
Definition of EllipseThis definition is illustrated for two ellipses with different eccentricities
|
Reflective Properties
|
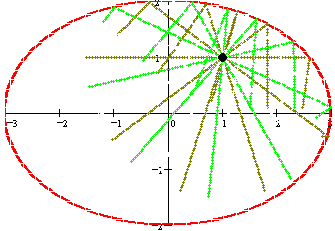 | |||||||||||
Cycloids and more...Note that the situations where the circle would get "stuck" in the base curve (e.g., due to the radius of curvature of B(t) becoming smaller than r) are not recognized. A physical interpretation of the resulting curve could be based on considering the 2-D picture to be a projection of a "thin" 3-D picture.
|
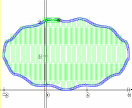
Area Inside a Parametric Curve
|
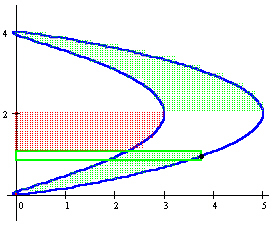 |
We illustrate the use of these formulas for calculation of area in the two examples below. Definite integrals
are approximated with the corresponding Riemann sums, and each animation frame corresponds to adding one term
to the sum. The area corresponding to the current term is enclosed in a rectangle - if the term is positive,
then the rectangle is green, otherwise it is red.
The partial sum of the terms included already is depicted using a dotted pattern - the dots are green within
region whose area is accounted for with a factor +1; the red dots correspond to regions accounted for with
a factor -1.
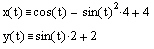 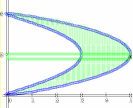 counterclockwise |
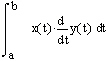
AVI file size: 134K (or try a shorter animation with 83K) |
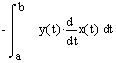
AVI file size: 166K (or try a shorter animation with 102K) |
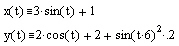  clockwise |
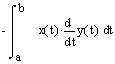
AVI file size: 75K |
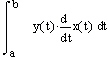
AVI file size: 73K |
 |
Polar Curves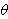 and
and 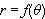 will be tabulated. Animations of the following
polar curves are available:
will be tabulated. Animations of the following
polar curves are available:
| ||||||||||||||||||||||||||||||
Quadric Surfaces
| |||||||||||||